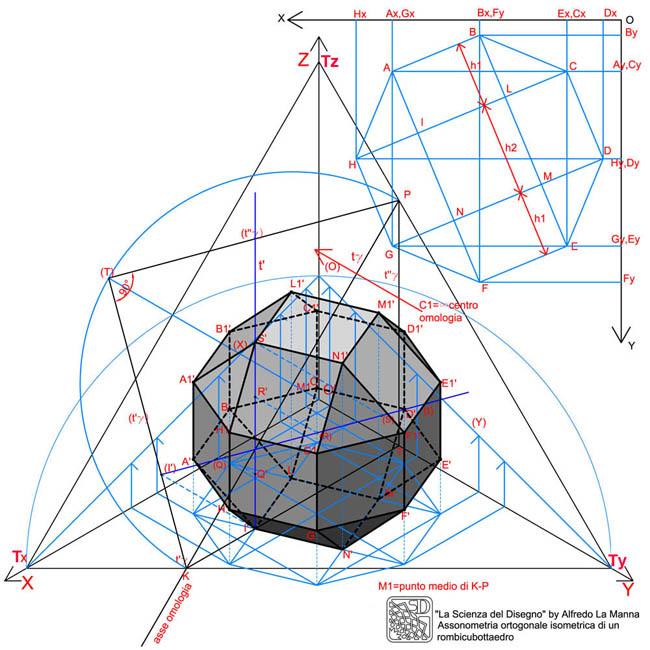
Assonometria ortogonale isometrica di un rombicubottaedro

Il rombicubottaedro è un solido che fa parte della famiglia dei poliedri semiregolari. Esso è formato da ben 26 facce, di cui 18 quadrate e 8 triangolari equilatere. Se si immagina di posizionare il solido rispetto ai piani assonometrici in modo che esso risulti poggiante per una delle sue facce quadrate nel piano XY, allora i 48 vertici del solido possono disporsi solo su tre altezze diverse, oltre all'altezza zero per i primi quattro vertici appartenenti alla faccia coincidente con il piano assonometrico XY.
Come si può vedere nella illustrazione accanto, il solido in assonometria isometrica è stato posizionato come nel modo sopra descritto, ed è stato innanzitutto rappresentato in proiezione ortogonale, secondo la vista dall'alto, in modo da disegnare preventivamente il suo schema planimetrico. Per la costruzione di tale schema, si può partire da un ottagono e collegare i vertici di esso come illustrato in figura. Tale schema è importante perchè riassume sostanzialmente le caratteristiche geometriche salienti del solido, come ad esempio le altezze caratteristiche secondo cui si dispongono tutti i vertici del solido in oggetto (h1 e h2).
Nella stessa rappresentazione in proiezione ortogonale sono stati anche rappresentati gli assi assonometrici e su di essi sono stati proiettati i vertici dello schema ottagonale, in modo da ricavarne le coordinate. Tali coordinate (ad es. le coordinate (Bx,Fx-Fy) individuano il punto F), sono state successivamente riportate sugli assi ribaltati (X) e (Y) e proiettate in direzione parallela all'asse Z sui rispettivi assi in assonometria. In tal modo, riportando sugli assi assonometrici le misure dagli assi ribaltati, si può tener conto del giusto fattore di riduzione assonometrica, che per l'assonometria isometrica è di circa 0,81.
Ricostruito lo stesso schema planimetrico anche in proiezione assonometrica, basta individuare le altezze h1 e h2 sulle verticali passanti dai punti di tale schema in assonometria. Per trovare h1 e h2 in assonometria ho ribaltato sul quadro assonometrico il piano γ facendolo ruotare attorno alla sua traccia tγ; insieme a tale piano ha subito lo stesso ribaltamento anche la retta t ad esso appartenente, passante per uno dei vertici della faccia quadrata interna del solido che risulta poggiante su XY. Sulla retta (t) ribaltata sono stati individuati i punti (I), (Q), (R) ed (S), in modo che (I)-(Q)=h1, (Q)-(R)=h2, (R)-(S)=h1.
Proiettando quindi tali punti sulla retta t in assonometria, sfruttando anche le proprietà dell'omologia di ribaltamento di centro C1 e asse coincidente con tγ, otterremo tali altezze fondamentali anche in assonometria sulla retta t, che potranno essere riportate su tutte le altre verticali (parallele a t) per individuare tutti i vertici del solido nella giusta posizione nello spazio.
Per seguire meglio tutte le fasi di costruzione del disegno, ti consiglio di consultare l'apposito pdf multipagina scaricabile.