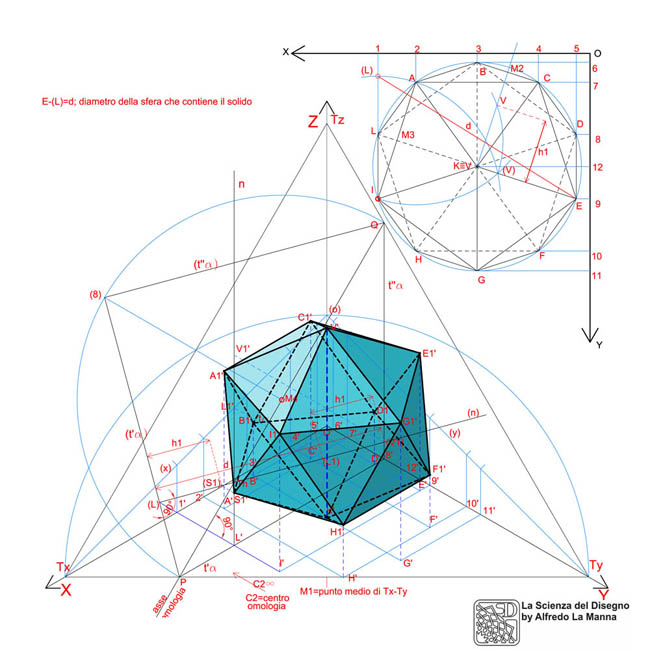
Assonometria ortogonale isometrica di un icosaedro

L'icosaedro è un poliedro regolare facente parte della ristretta famiglia dei solidi platonici, che possiede venti facce triangolari equilatere, trenta spigoli e dodici vertici. Per la sua costruzione tridimensionale ti consiglio di consultare anche l'esercizio “Proiezioni ortogonali di un icosaedro” (sez. 2, gruppo 2) in questo stesso sito.
Come puoi vedere nel disegno a fianco, il solido è stato posizionato rispetto ai piani assonometrici in modo da avere un vertice coincidente con il piano XY e il diametro che passa per tale vertice ed il suo opposto risulta ortogonale a tale piano. Con il solido in questa posizione i suoi vertici possono avere solo tre altezze diverse, oltre all'altezza zero (vertice inferiore coincidente con XY).
Innanzitutto rappresentiamo il solido con gli assi assonometrici in proiezione ortogonale, secondo la vista dall'alto, in modo da disegnare il suo schema planimetrico, ove sono proiettati in piano tutti i suoi vertici e spigoli.
Il procedimento seguito è lo stesso di quello che ho già usato per l'assonometria isometrica dell'ottaedro e rombicubottaedro (vedi relativi esercizi e testo esplicativo in questa stessa sezione). Dopo aver individuato sugli assi ribaltati (X) e (Y) le coordinate dei vertici riportandole dallo schema planimetrico, esse sono state quindi proiettate (in direzione ortogonale alla traccia di XY passante per Tx e Ty) sugli stessi assi in assonometria, in modo da ricostruire lo stesso schema planimetrico anche in proiezione assonometrica.
Presta particolare attenzione al modo in cui è stata eseguita nello schema planimetrico la costruzione per ricavare sia il diametro della sfera in cui il solido e inscritto (che equivale all'altezza massima), sia la distanza verticale h1 dei due gruppi di vertici intermedi (cinque per ciascun gruppo) dai due vertici inferiore e superiore K e V appartenenti al diametro del solido (o della sfera che lo contiene) perpendicolare al piano XY.
Per riportare in assonometria le altezze fondamentali d e h1, è stato eseguito il ribaltamento del piano α e della retta n ad esso appartenente e passante per il punto L′ sullo schema planimetrico. Trovati S1, V1 e L1 sulla (r) ribaltata, distanti da (L) ribaltato rispettivamente della quantità h1, d e d-h1, si troveranno i loro corrispondenti S1′, V1′ e L1′ sulla retta r in assonometria attraverso l'omologia di ribaltamento di centro C1 e asse coincidente con la traccia tα. Con questo procedimento, basato sul ribaltamento degli assi e della retta verticale sulla quale riportare le altezze fondamentali, tutte le misure del disegno in assonometria vengono scalate secondo il coefficiente di riduzione assonometrica, che per l'assonometria isometrica è di circa 0,81. Per rappresentare correttamente tutti gli spigoli del solido devi collegare correttamente i vertici di esso tenendo conto degli stessi collegamenti precedentemente rappresentati nello schema planimetrico.
Ti ricordo che se vuoi seguire in maniera più dettagliata tutte le fasi di costruzione del disegno, puoi scaricare il file pdf multipagina.