Raccordare una spezzata

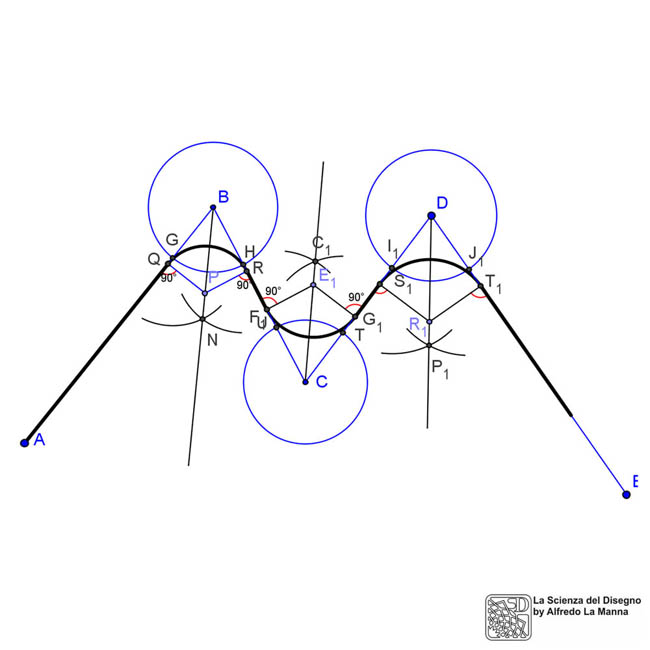
Data una linea spezzata di vertici interni B, C, e D, ci si propone di trovare tre archi di cerchio di raggio qualsiasi che raccordino i segmenti nei vertici suddetti. Naturalmente gli archi di raccordo devono essere tali che le loro tangenti nei punti di raccordo con i segmenti devono coincidere con i segmenti medesimi, altrimenti il passaggio dal segmento retto all'arco genererebbe una cuspide con una discontinuità.
Per rispettare questa proprietà geometrica, basta individuare i centri degli archi sulle bisettrici degli angoli ai vertici. Per trovare le bisettrice nell'angolo in B, ad esempio, basta tracciare un cerchio (o arco di cerchio) con centro sul vertice B, in modo da individuare i punti G, H. Da questi ultimi fare centro per tracciare due archi di raggio uguale, dalla cui intersezione troveremo il punto N. Dal punto N passa proprio la bisettrice dell'angolo in B; su tale bisettrice potremo quindi scegliere a piacere un punto qualsiasi, nel nostro caso il punto P, da cui fare centro per disegnare l'arco di raccordo.
Prima di tracciare l'arco per raccordare i segmenti convergenti in B, è necessario individuare i punti di raccordo tracciando le perpendicolari ai segmenti considerati per il punto P. I punti di raccordo appartengono sia ai segmenti che alle perpendicolari appena tracciate, nel nostro caso i punti Q ed R. Da questi ultimi passano proprio gli archi di raccordo cercati. Con lo stesso procedimento si troveranno gli archi di raccordo nei vertici C e D.
Puoi scaricare il file in formato .ggb (geogebra) se intendi seguire tutta la costruzione in sequenza, dall'inizio alla fine del disegno.