Prospettiva di un cono

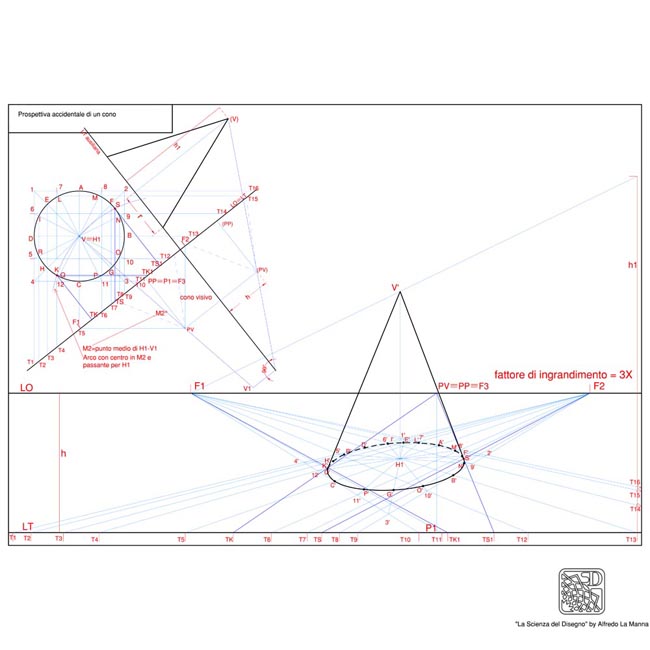
L'esercitazione illustrata nel disegno a fianco riguarda la rappresentazione in prospettiva a quadro verticale di un cono con base poggiante sul piano geometrale, utilizzando il consueto metodo del disegno preparatorio per la definizione di tutti gli elementi utili per la restituzione prospettica. Ti consiglio di consultare anche il file pdf multipagina per seguire tutte le fasi dell'esercitazione.
Nel disegno preparatorio il cono ed il punto di vista sono stati rappresentati in vista orizzontale e nella vista ausiliaria di profilo, essendo quest'ultima necessaria per impostare le altezze del solido e di PV. La base circolare del cono è stata inscritta in un quadrato, i cui lati sono stati suddivisi in quattro parti, ottenendo così tre punti di suddivisione intermedi su ogni lato oltre ai quattro punti sui vertici del quadrato medesimo.
Le radiali che collegano i punti di suddivisione opposti e le mediane del quadrato si intersecano col cerchio generando i punti contrassegnati con le lettere A, B,....R, che devono essere individuati anche nella restituzione prospettica per ricostruire la base circolare del cono in prospettiva (passo 5/23 del pdf multipagina). Per ottenere dunque questi punti appartenenti alla base circolare del cono anche nella vista prospettica, è necessario considerare una serie di rette passanti per ciascuno di essi e assegnando a ciascuna di queste rette una delle due direzioni parallele ai lati del quadrato (passo 6/23); rappresentando in prospettiva queste rette, tali punti saranno individuati facilmente dalla loro intersezione con le radiali precedentemente trovate all’interno del quadrato in prospettiva (passo 14/23).
La base circolare del cono in prospettiva deve passare per i punti precedentemente individuati e sarà abbastanza simile ad una ellisse leggermente deformata. Un cerchio rappresentato in prospettiva non può mai essere difatti una ellisse perfetta, come avviene invece nelle proiezioni assonometriche.
Per completare la prospettiva del cono è necessario trovare i bordi della superficie conica che risultano tangenti alla base e convergenti nel vertice V del cono medesimo. Questi sono determinati dalle rette di tangenza alla falda del cono dei due piani proiettanti passanti per PV, il vertice V e i punti K ed S alla base circolare del solido. Per poter disegnare i bordi della superficie del cono è dunque necessario individuare questi punti di tangenza alla base K ed S. A tale scopo consideriamo, nel disegno preparatorio, la retta passante dal vertice V del cono e da PV e troviamo il punto V1 di intersezione di tale retta col piano geometrale (passo 16/23): dobbiamo a questo punto applicare la nota costruzione per trovare le tangenti ad un cerchio passanti da un punto esterno (vedi anche sez. 1, gruppo 2: tangenti ad un cerchio passanti per un punto esterno), ove in questo caso il punto esterno è V1 (passo 18/23).
I punti K ed S così trovati nel disegno preparatorio debbono adesso essere individuati anche nella restituzione prospettica come intersezione delle due coppie di rette le cui tracce sulla LT sono, rispettivamente, TK, TK1 per il punto K e TS, TS1 per il punto S (passo 22/23); basta infine collegare V' (prospettiva del vertice V) con i punti di tangenza K ed S per trovare in prospettiva i bordi laterali del cono (passo 23/23), completando così l'esercitazione.